Transpose of a matrix is obtained by interchanging it's rows and columns. The transpose of a matrix A of size m x n) is denoted by AT and is a matrix of size n x m where each element ATij is equal to the corresponding element Aji in the original matrix.
ATij = Aji
Figure below shows an example of matrix and its transpose.
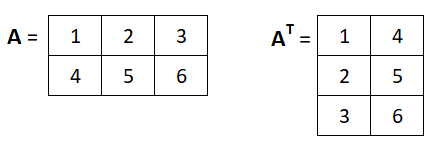
The steps to find the transpose of a matrix are as below:
Initialize a new matrix of size n x m, where n and m are the number of rows and columns in the original matrix respectively.
For each element in the original matrix, copy it to the corresponding position in the transpose, but with the rows and columns switched. For example, the element aij in the original matrix becomes aji in the transpose.
C program
Here is a sample C program to find the transpose of a matrix. This program first prompts the user to enter the number of rows and columns in the matrix and its elements. Then, it calculates the transpose of the matrix by interchanging the rows and columns of the original matrix and finally prints the transpose.
#include <stdio.h>
#define MAX 10
int main() {
int row, col;
int a[MAX][MAX], atranspose[MAX][MAX];
// Read the matrix
printf("Enter rows and columns of the matrix: ");
scanf("%d%d", &row, &col);
printf("Enter elements of the matrix:\n");
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
scanf("%d", &a[i][j]);
//Initialize the result matrix to 0
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
atranspose[j][i] = a[i][j];
// Print result matrix
printf("Transpose of the matrix:\n");
for (int i = 0; i < col; i++){
for (int j = 0; j < row; j++)
printf("%d ", atranspose[i][j]);
printf("\n");
}
return 0;
}The output from the above program will like this:
Enter rows and columns of the matrix: 2 3 Enter elements of the matrix: 1 2 3 4 5 6 Transpose of the matrix: 1 4 2 5 3 6



