A binary search algorithm is an algorithm to search the position of an element inside a sorted array. The following are the steps in a binary search.
- Get middle element of the array.
- If the middle element is the search element then return the position and end the search.
- If the search element is greater than the middle element, then cut the array in two halves and continue searching the upper half.
- If the search element is lower than the middle element then search the lower half of the array.
- Repeat the above steps until the search element is found or the search range is empty.
Example of a binary search
Consider an array of six elements in the sorted order as below. Let's say you want to find the position of 85 in this array.

In the above array, A0 (element at index position 0) is the lowest element in the array and A5 (element at index position 5) is the highest element in the array as this is an array sorted in ascending order.
Length of array (len) = 7 Lowest Element Position (low) = 0 Highest Element Position (high) = len - 1 = 6 Lowest Element = Alow = A0 21 Highest Element = A(high) = A6 = 90
The Binary Search algorithm gets the middle element in the array, and splits the array in two halves. The lower half starts from the lowest array element up to the middle element. Upper half starts from the element after the middle element up to the highest element.
Middle Element Position (mid) = (low+high) / 2 = 3 Middle Element = A(mid) = A3 = 58
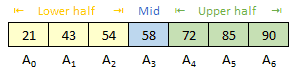
58 is less than the search element 85, so you only need to search for 85 in the upper half of the array.

The same process is now repeated on the upper sub-array.
Lowest Element Position(low) = mid+1 = 4 Highest Element Position(high) = 6 Middle Element Position (mid) = (low+high) / 2 = 5 Lowest Element = Alow = A4 = 72 Highest Element = Ahigh = A6 = 90 Middle Element = Amid = A5 = 85
The middle element of the sub array is 85, which is our search element. So the search ends here and the index position, which is 5 is returned.
Binary Search C Program
Below is a C program to do a Binary search on an array of integers that is sorted in ascending order.
#include <stdio.h>
int binarysearch(int a[], int len, int x) {
int low = 0;
int high = len - 1;
int mid;
while (low <= high) {
mid = (low + high) / 2;
if (a[mid] == x)
return mid;
if (a[mid] < x)
low = mid + 1;
else
high = mid - 1;
}
return -1;
}
int main(void) {
int a[100];
int len, pos, search_item;
printf("Enter the length of the array\n");
scanf("%d", &len);
printf("Enter the array elements\n");
for (int i=0; i<len; i++)
scanf("%d", &a[i]);
printf("Enter the element to search\n");
scanf("%d", &search_item);
pos = binarysearch(a,len,search_item);
if (pos < 0 )
printf("Cannot find the element %d in the array.\n", search_item);
else
printf("The position of %d in the array is %d.\n", search_item, pos+1);
return 0;
}
Sample Output
Enter the length of the array 5 Enter the array elements 12 16 21 32 54 Enter the element to search 16 16 is in position 2 in the array
If your array is sorted in descending order you only need to change one line in the above program.
if (a[mid] < x) low = mid + 1; else high = mid - 1;
Change to
if (a[mid] > x)
low = mid + 1;
else
high = mid - 1;



